キラーナンプレ 解き方のコツ 攻略
ナンプレに+αの機能が追加された「キラーナンプレ」の解き方のコツをまとめました!
難易度エキスパートでも使える解き方を紹介しています?
今から紹介する他にも「こんな解き方があるよ!」という方は、コメント欄から教えていただけるとありがたいです!
キラーナンプレの解き方
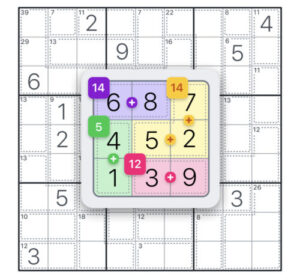
一般的なナンプレの解き方は縦、横、そして同じ9つに分かれたブロックに同じ数字が入らないように、当てはめていきます。
しかし、キラーナンプレでは上記に加えて「ケージ」と呼ばれるマスのくくりは、マス同士で合わせた合計はケージに書かれた数字より大きいことが許されません。
そして、ケージの中にも同じ数字は入れることができません。
2マスであれば14=?+?、3マスであれば14=?+?+?となるように当てはめます。
また1列、1ブロックのマスの合計は45となります。
解き方のコツ 初級編

ケージ内が残り1マス
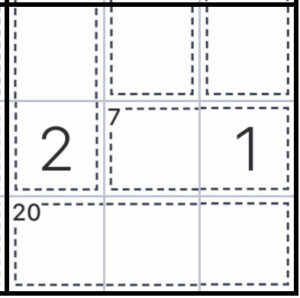
7と書かれたケージには1という数字がすでに入っています。
もうこのマスには6しか入らないので、このマスは6で確定です。
このようにケージ内のマスが残り1マスなら引き算で簡単に求めることができます。
同じ列と行、ブロックで1マスだけ仲間はずれ
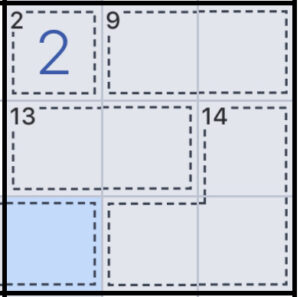
これは1列やブロックの中で1マスだけ何が入るかわからない時に使えます。
青く選択されたマス以外は全てのケージがブロック内に収まっているため、計算をすると当てはめることができます。
2+9+13+14=38
選択されたマスに当てはまる数
45-38-7
A.選択したマスには7が入る。

行や列も同じで、その1列に1マス以外ケージが全て収まっていれば、選択しているマスを求めることができます。
12+5+12+15=44
選択されたマスに当てはまる数
45-44=1
A.選択したマスには1が入る。
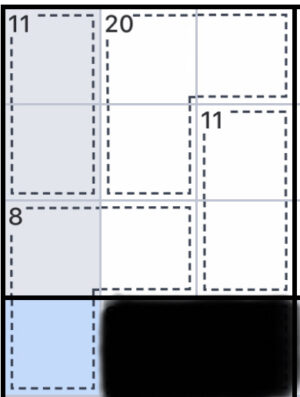
この写真の時はブロック外にある選択されたマスを求めることができます!
実際にブロック内には11と11と20のケージと途切れている8のケージがあります。
今からする求め方は、ブロック内の途切れているケージにあるマスが1つ以上で、外にあるマスが1つの場合成立します!
11+11+20=42
ブロック内にある8のケージの2マスの合計
45-42=3
選択されたマスに当てはまる数
8-3=5
A.選択されたマスには5が入る。
解き方のコツ 中級編

ケージの中に1通りの組み合わせしか入らない
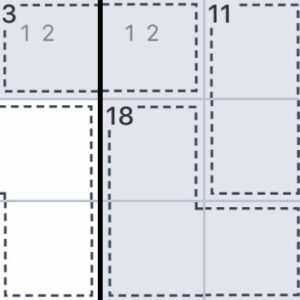
写真の3と書かれているケージは1と2の組み合わせしか入れることが出来ません。
ここにどちらかが1でどちらかが2と分かると、同じ列やブロックには1と2が入ることはないので、数字を埋めやすくなります?
3 ・・・1と2
4 ・・・1と3
16・・・7と9
17・・・8と9
6 ・・・1と2と3
7 ・・・1と2と4
23・・・6と8と9
24・・・7と8と9
絶対にそのマスに当てはまらない数
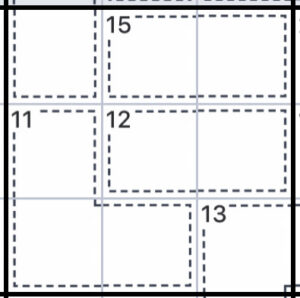
ケージの数によってはそのマスには絶対に当てはめれない数が存在します。
上の写真を見ると、15と書かれた2マスで形成されたケージがあります。
このマスには2つの数字で15にしなければならないので、1,2,3,4,5が当てはまりません。
上の写真の12のケージも同様に、2つの数で12を作らなければならないので、1,2が当てはまりません。
こんな感じで2マスである数字をを入れた場合、残りの数字でケージの数を作れるかなという風に考えれば、2マス同様3マスも4マスのケージも同じ考えで当てはめれます。(4マスのケージでこの考えはほとんどない)
ケージが17のマスには1,2,3,4,5,6,7が入らない。
解き方のコツ 上級編

同じ列と行、ブロックの中に同じ数とマス数のケージ
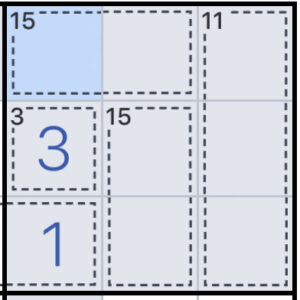
この例は珍しいですが、同じ列や同じブロックに同じ数とマス数のケージがあることがあります。
この時に2通りの組み合わせしか当てはめられないケージであれば、この方法は使えます。
上の写真の場合、15と書かれたケージが2つあります。
このケージに当てはまる数字の組み合わせは、9と6、8と7のみです。
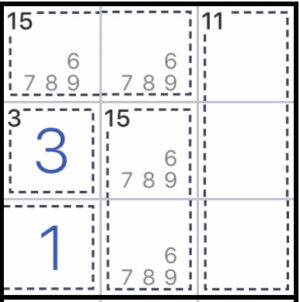
これをメモで書くと、写真のようになります。
2通りしか当てはめることはできないので、6,7,8,9は使ったことになり、他のマスには6,7,8,9以外の数字が入ることになるので、埋めやすくなりますね?
これは2通りの数字の組み合わせが当てはまるケージならどれでも出来るので、試してみて下さい!
3通りがのケージが同じブロックなどに入ってくることはありません?♂️
ケージの片方に2通りの数字が入る場合があるとき
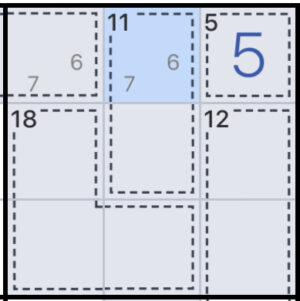
上の写真のように左上2マスには6か7が入ることが確定しているとき、11と書かれたケージに6の場合と7の場合どっちが入るか求めることが出来るかもしれません。
11のケージに7を当てはめた場合、11-7=4 でもう一方のマスには4が入ることが分かります。
11のケージに6を当てはめた場合、11-6=5 でもう一方のマスには5が入ることが分かります。
しかし、5は既に同じブロック内に当てはめてあるので、使えません❌
よって11のケージに入る数は、上のマスに7、下のマスに4ということが分かりました!
こんな感じで「~の場合」という風に考えると埋めることがあるので、ぜひ使ってみて下さい!
他にも「こんな解き方あるよ!」という方は、コメント欄で教えていただけるとありがたいです?













コメント
コメント一覧 (3件)
初級編のテクニックと同じかもしれませんが、
(同じ列と行、ブロックで1マスだけ仲間はずれの箇所です。)
このやり方は、2行内、2列内、2ブロック内などでも使えます。
1行内だと全て足すと45ですが、2行だと90になる違いがあるだけでやり方は同じです。
とりあえず、1行でも2行でも3行でも、1マスだけ仲間はずれがあれば、
n行でもn列でもnブロックでも、n×45から引けば良いと思います。
■凸と凹が1マスずつの場合
出てるマスと凹んでる部分のマスの差がわかる。差が8なら1と9が確定する。
■同数2マス枠の縦横ぶつかり
□
□・・・・・・□□
みたいな形の場合、同じ組み合わせはありえない
初級編のテクニックの応用ですが
ブロック内に収まっていないマスが2マスなら、2マスのケージ
ブロック内に収まっていないマスが3マスなら、3マスのケージ
と同じように扱えます(マス同士が離れていてもOKです)。
例えばブロック内に収まっていないマスが2マスでその合計が16なら
その2マスに入る数は7と9の組み合わせと分かります。
ブロック外にはみでた複数のマスも、同じブロック、列、行に属しているなら同様に扱えますが
属していない場合、同じ数が入る可能性も考える必要があります。
上の例のように2マスの合計が16なら、7と9、8と8、どちらかの組み合わせになります。